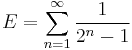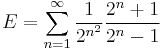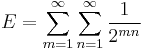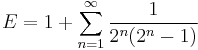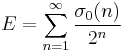Erdős–Borwein constant

The Erdős–Borwein constant is the sum of the reciprocals of the Mersenne numbers. It is named after Paul Erdős and Peter Borwein.

By definition it is:

E=\sum_{n=1}^{\infty}\frac{1}{2^n-1}

which is approximately 1.60669 51524 15291 763… (sequence A065442 in OEIS).

It can be proven that the following forms are equivalent to the former:

E=\sum_{n=1}^{\infty}\frac{1}{2^{n^2}}\frac{2^n%2B1}{2^n-1}
E=\sum_{m=1}^{\infty}\sum_{n=1}^{\infty} \frac{1}{2^{mn}}
E=1%2B\sum_{n=1}^{\infty} \frac{1}{2^n(2^n-1)}
E=\sum_{n=1}^{\infty}\frac{\sigma_0(n)}{2^n}

where σ0(n) = d(n) is the divisor function, a multiplicative function that equals the number of positive divisors of the number n. To prove the equivalence of these sums, note that they all take the form of Lambert series and can thus be resummed as such.

Erdős in 1948 showed that the constant E is an irrational number.

External links